ДВУМЕРНЫЕ ИНТЕГРАЛЬНЫЕ ПРЕОБРАЗОВАНИЯ С ФУНКЦИЕЙ КУММЕРА И ГИПЕРГЕОМЕТРИЧЕСКОЙ ФУНКЦИЕЙ ГАУССА В ЯДРАХ КАК ЧАСТНЫЕ СЛУЧАИ ДВУМЕРНОГО ИНТЕГРАЛЬНОГО G-ПРЕОБРАЗОВАНИЯ
##plugins.themes.bootstrap3.article.sidebar##
##plugins.themes.bootstrap3.article.main##
Аннотация
Рассматриваются два двумерных интегральных преобразования с вырожденной гипергеометриче- ской функцией Куммера и гипергеометрической функцией Гаусса в ядрах. Применяя технику преобразования Меллина, показываем, что они являются частными случаями двумерного G-преобразования. На основании теории G-преобразования в работе исследованы свойства рассматриваемых интегральных преобразований в весовых пространствах интегрируемых функций в области 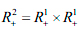 . Результаты исследования обобщают полученные ранее для соответствующих одномерных аналогов.
. Результаты исследования обобщают полученные ранее для соответствующих одномерных аналогов.
##plugins.themes.bootstrap3.article.details##

Это произведение доступно по лицензии Creative Commons «Attribution» («Атрибуция») 4.0 Всемирная.
С. М. СИТНИК, Белгородский государственный национальный исследовательский университет, Россия
д-р физ.-мат. наук, доц.
О. В. СКОРОМНИК, Полоцкий государственный университет имени Евфросинии Полоцкой
канд. физ.-мат. наук, доц.
Библиографические ссылки
Papkovich, M. V., & Skoromnik, O. V. (2019). Dvumernoe integral'noe preobrazovanie s G-funktsiei Meiera v yadre v prostranstve summiruemykh funktsii [Two-Dimentional Integral Transform With the Meijer G-Function in the Kernel in the Space of Summable Functions]. Vestnik Polotskogo gosudarstvennogo universiteta. Seriya C, Fundamental'nye nauki [Herald of Polotsk State University. Series С. Fundamental sciences], (4), 131–136. (In Russ., abstr. in Engl.).
Sitnik, S. M., Skoromnik, O. V., & Papkovich, M. V. (2022). Dva chastnykh sluchaya dvumernogo integral'nogo G-preobrazovaniya v vesovykh prostranstvakh summiruemykh funktsii [Two special cases of two-dimensional integral G-transformation in the weighted spaces of summable functions]. Vestnik Polotskogo gosudarstvennogo universiteta. Seriya C, Fundamental'nye nauki [Herald of Polotsk State University. Series С. Fundamental sciences], (11), 117–123. (In Russ., abstr. in Engl.). DOI: 10.52928/2070-1624-2022-39-11-117-123.
Skoromnik, O. V., & Papkovich, M. V. (2022). Mnogomernye modifitsirovannye G-preobrazovaniya i integral'nye preobrazovaniya s gipergeometricheskoi funktsiei Gaussa v yadrakh v vesovykh prostranstvakh summiruemykh funktsii [Multidimensional modified G-transformations and integral transformations with hypergeometric Gauss functions in kernels in weight spaces of summed functions]. Vesnіk Vіtsebskaga dzyarzhaunaga unіversіteta [Bulletin of VSU], 1(114), 11–25. (In Russ., abstr. in Engl.).
Sitnik S. M., Skoromnik, O. V., & Papkovich, M. V. (2022). Mnogomernye modifitsirovannye G- i H-preobrazovaniya i ikh chastnye sluchai [Multidimensional modified G- and H-transforms and their special cases]. In AMADE-2021: sb. trudov (104–116). Minsk: IVTs Minfina. (In Russ., abstr. in Engl.).
Sitnik, S. M., Skoromnik, O. V., & Shlapakov, S. A. (2019). Mnogomernoe obshchee integral'noe preobrazovanie so spetsial'nymi funktsiyami v yadre [Multidimensional general integral transformation with special functions in the kernel]. Vesnіk Vіtsebskaga dzyarzhaunaga unіversіteta [Bulletin of VSU], 3(104), 18–27. (In Russ., abstr. in Engl.).
Sitnik, S. M., & Skoromnik, O. V. (2020). One-dimensional and multi-dimensional integral transforms of Buschman-Erdelyi type with Legendre Functions in kernels. In Transmutation Operators and Applications. Trends in Mathematics (293–319). Cham, Switzerland: Birkhäuser Basel (Springer).
Samko, S. G., Kilbas, A. A., & Marichev, O. I. (1987). Integraly i proizvodnye drobnogo poryadka i nekotorye ikh prilozheniya [Integrals and derivatives of fractional order and some of their applications]. Minsk: Nauka i tekhnika. (In Russ.).
Beitmen, G., & Erdeii, A. (1973). Vysshie transtsendentnye funktsii: v 3 t. T. 1: Gipergeometricheskaya funktsiya Gaussa. Funktsiya Lezhandra. Moscow: Nauka. (In Russ.).
Kilbas, A. A., & Saigo, M. H. (2004). H-Transforms. Theory and Applications. London [etc.]: Chapman and Hall. CRC Press.
Sitnik, S. M., Skoromnik, O. V., & Shlapakov, S. A. (2022). Multi-dimensional generalized integral transform in the weighted spaces of summable functions. Lobachevskii J. of Mathematics, 43(6), 1170–1178.
Kilbas, A. A., Srivastava, H. M., & Trujillo, J. J. (Ed.). (2006). Theory and applications of fractional differential equations. North–Holland Mathematics Studies (Vol. 204). Amsterdam: Elsevier.xv.
Prudnikov, A. P., Brychkov, Yu. A., & Marichev, O. I. (1986). Integraly i ryady: v 3 t. T. 3: Dopolnitel'nye glavy. Moscow: Nauka. (In Russ.).
Рекомендуемые статьи автора (авторов)
- М. В. ПАПКОВИЧ, О. В. СКОРОМНИК, С. А. ШЛАПАКОВ, РЕШЕНИЕ ОДНОГО КЛАССА МНОГОМЕРНЫХ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ ПЕРВОГО РОДА С ФУНКЦИЕЙ ГИПЕРБОЛИЧЕСКОГО СИНУСА В ЯДРАХ, Вестник Полоцкого государственного университета. Серия С. Фундаментальные науки: № 12 (2021)
- С. М. СИТНИК, О. В. СКОРОМНИК, Е. Н. АРХИПОВЕЦ, ОДНО ОБОБЩЕННОЕ H-ПРЕОБРАЗОВАНИЕ В ВЕСОВЫХ ПРОСТРАНСТВАХ ИНТЕГРИРУЕМЫХ ФУНКЦИЙ НА ПОЛУОСИ, Вестник Полоцкого государственного университета. Серия С. Фундаментальные науки: № 12 (2021)
- С. М. СИТНИК, О. В. СКОРОМНИК, М. В. ПАПКОВИЧ, ДВУМЕРНОЕ ИНТЕГРАЛЬНОЕ H-ПРЕОБРАЗОВАНИЕ В ВЕСОВЫХ ПРОСТРАНСТВАХ СУММИРУЕМЫХ ФУНКЦИЙ, Вестник Полоцкого государственного университета. Серия С. Фундаментальные науки: № 2 (2023)
- С. М. СИТНИК, О. В. СКОРОМНИК, М. В. ПАПКОВИЧ, ДВА ЧАСТНЫХ СЛУЧАЯ ДВУМЕРНОГО ИНТЕГРАЛЬНОГО G-ПРЕОБРАЗОВАНИЯ В ВЕСОВЫХ ПРОСТРАНСТВАХ СУММИРУЕМЫХ ФУНКЦИЙ, Вестник Полоцкого государственного университета. Серия С. Фундаментальные науки: № 11 (2022)
- М. В. ПАПКОВИЧ, О. В. СКОРОМНИК, ДВУМЕРНОЕ ИНТЕГРАЛЬНОЕ ПРЕОБРАЗОВАНИЕ С G-ФУНКЦИЕЙ МЕЙЕРА В ЯДРЕ В ПРОСТРАНСТВЕ СУММИРУЕМЫХ ФУНКЦИЙ, Вестник Полоцкого государственного университета. Серия С. Фундаментальные науки: № 4 (2019)
- О. В. СКОРОМНИК, ДВУМЕРНОЕ ИНТЕГРАЛЬНОЕ ПРЕОБРАЗОВАНИЕ С МОДИФИЦИРОВАННОЙ H-ФУНКЦИЕЙ В ПРОСТРАНСТВЕ СУММИРУЕМЫХ ФУНКЦИЙ, Вестник Полоцкого государственного университета. Серия С. Фундаментальные науки: № 4 (2018)
- О. В. СКОРОМНИК, ДВУМЕРНОЕ ИНТЕГРАЛЬНОЕ ПРЕОБРАЗОВАНИЕ С ВЫРОЖДЕННОЙ ГИПЕРГЕОМЕТРИЧЕСКОЙ ФУНКЦИЕЙ КУММЕРА В ЯДРЕ И ИНТЕГРАЛЬНОЕ УРАВНЕНИЕ ПЕРВОГО РОДА В ПРОСТРАНСТВЕ СУММИРУЕМЫХ ФУНКЦИЙ, Вестник Полоцкого государственного университета. Серия С. Фундаментальные науки: № 4 (2017)
- О. В. СКОРОМНИК, Т. А. АЛЕКСАНДРОВИЧ, РЕШЕНИЕ МНОГОМЕРНОГО ИНТЕГРАЛЬНОГО УРАВНЕНИЯ ПЕРВОГО РОДА С ФУНКЦИЕЙ БЕССЕЛЯ – КЛИФФОРДА В ЯДРЕ ПО ПИРАМИДАЛЬНОЙ ОБЛАСТИ, Вестник Полоцкого государственного университета. Серия С. Фундаментальные науки: № 4 (2015)
- О. В. СКОРОМНИК, ИНТЕГРАЛЬНЫЕ ПРЕОБРАЗОВАНИЯ С ВЫРОЖДЕННОЙ ГИПЕРГЕОМЕТРИЧЕСКОЙ ФУНКЦИЕЙ КУММЕРА И НОРМИРОВАННОЙ ФУНКЦИЕЙ БЕССЕЛЯ В ЯДРАХ И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО РОДА В ПРОСТРАНСТВЕ СУММИРУЕМЫХ ФУНКЦИЙ, Вестник Полоцкого государственного университета. Серия С. Фундаментальные науки: № 12 (2016)
- О. В. СКОРОМНИК, РЕШЕНИЕ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ ПЕРВОГО РОДА С ВЫРОЖДЕННОЙ ГИПЕРГЕОМЕТРИЧЕСКОЙ ФУНКЦИЕЙ И НОРМИРОВАННОЙ ФУНКЦИЕЙ БЕССЕЛЯ В ЯДРАХ В КЛАССЕ ИНТЕГРИРУЕМЫХ ФУНКЦИЙ, Вестник Полоцкого государственного университета. Серия С. Фундаментальные науки: № 12 (2015)



