TWO-DIMENTIONAL INTEGRAL TRANSFORM WITH THE MEIJER G-FUNCTION IN THE KERNEL IN THE SPACE OF SUMMABLE FUNCTIONS
Article Sidebar
Main Article Content
Abstract
Two-dimentional integral transform with the Meijer G-function in the kernel in the space of summable functions on a domain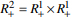 
was studied. 
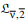-theory of a considered integral transformation was constructed. Conditions for the boundedness and one-to-one operator of such a transformation from one 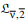-space to another were given, an analogue of the integration formula in parts was proved, various integral representations for the transformation under consideration were established. The results generalize the well know findings for corresponding one-dimentional integral transform.
Article Details
This work is licensed under a Creative Commons Attribution 4.0 International License.
References
Самко, С.Г. Интегралы и производные дробного порядка и некоторые их приложения / С.Г. Самко, А.А. Килбас, О.И. Маричев. – Минск : Наука и техника, 1987. – 688с.
Kilbas, A.A. H-Transforms. Theory and Applications / A.A. Kilbas, M.H. Saigo. – London [etc.] : Chapman and Hall. CRC Press, 2004. – 401 p.
Kilbas, A.A. Theory and applications of fractional differential equations. North – Holland Mathematics Studies 204 / A.A. Kilbas, H.M. Srivastava, J.J. Trujillo. – Amsterdam : Elsevier.xv, 2006. – 523 p.