TWO-DIMENSIONAL INTEGRAL H-TRANSFORM IN WEIGHTED SPACES OF SUMMABLE FUNCTIONS

Article Sidebar

Abstract views: 115
PDF Downloads: 58
pdf (rus) (Русский)
Published: Oct 31, 2023
DOI: https://doi.org/10.52928/2070-1624-2023-41-2-93-103
Keywords:
двумерное интегральное H-преобразование, пространство интегрируемых функций, специальные функции в ядрах, двумерное преобразование Меллина, дробные интегралы и производные two-dimensional integral H-transform, space of integrable functions, special functions in kernels, two-dimensional Mellin transform, fractional integrals and derivatives
Issue
No. 2 (2023)
Section
mathematics

Main Article Content

S. SITNIK
Belgorod State National Research University "BelGU"
O. SKOROMNIK
Euphrosyne Polotskaya State University of Polotsk
M. PAPKOVICH
Euphrosyne Polotskaya State University of Polotsk

Abstract

Two-dimensional integral H-transform in spaces of integrable functions 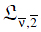has been studied. Conditions for the boundedness and one-to-one action of the operator of such a transform from one 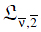- space to another have been obtained, an analogue of the formula for integration by parts has been proven, and various integral representations have been established for the transformation under consideration. The results of the study generalize those previously obtained for the corresponding one-dimensional transform.

Article Details

How to Cite
SITNIK, S., SKOROMNIK, O., & PAPKOVICH, M. (2023). TWO-DIMENSIONAL INTEGRAL H-TRANSFORM IN WEIGHTED SPACES OF SUMMABLE FUNCTIONS. Vestnik of Polotsk State University. Part C. Fundamental Sciences, (2), 93-103. https://doi.org/10.52928/2070-1624-2023-41-2-93-103
Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

Author Biographies

S. SITNIK, Belgorod State National Research University "BelGU"

д-р физ.-мат. наук, доц.

O. SKOROMNIK, Euphrosyne Polotskaya State University of Polotsk

канд. физ.-мат. наук, доц.

Crossref
Scopus
Google Scholar
Europe PMC

References

Sitnik, S. M., & Skoromnik, O. V. (2020). One-Dimensional and Multi-Dimensional Integral Transforms of Buschman–Erdélyi Type with Legendre Functions in Kernels. In V. Kravchenko, & S. Sitnik (Eds.), Transmutation Operators and Applications. Trends in Mathematics (293–319). Birkhäuser, Cham. DOI: 10.1007/978-3-030-35914-0_13.

Sitnik, S. M., Skoromnik, O. V., & Shlapakov, S. A. (2022). Multi-Dimensional Generalized Integral Transform in the Weighted Spaces of Summable Functions. Lobachevskii J. Math, 43(6), 1408–1416. DOI: 10.1134/S1995080222090244.

Samko, S. G., Kilbas, A. A., & Marichev, O. I. (1993). Fractional Integrals and Derivatives: Theory and Applications. Switzerland; Philadelphia, Pa., USA: Gordon and Breach Science Publishers.

Kilbas, A. A., Srivastava, H. M., & Trujillo, J. J. (2006). Theory and applications of fractional differential equations. North-Holland Mathematics Studies: vol. 204. Elsevier. DOI: 10.1016/S0304-0208(06)80001-0.

Skoromnik, O. V., & Papkovich, M. V. (2022). Mnogomernye modifitsirovannye G-preobrazovaniya i integral'nye preobrazovaniya s gipergeometricheskoi funktsiei Gaussa v yadrakh v vesovykh prostranstvakh summiruemykh funktsii [Multidimensional modified G-transformations and integral transformations with hypergeometric Gauss functions in kernels

in weight spaces of summed functions]. Vesnіk Vіtsebskaga dzyarzhaunaga unіversіteta [Bulletin of VSU], 1(114), 11–25. (In Russ., abstr. in Engl.).

Sitnik, S. M., Skoromnik, O. V., & Papkovich, M. V. (2022). Mnogomernye modificirovannye G- i H-preobrazovanija i ih chastnye sluchai [Multidimensional Modified G- and H-Transforms and Their Special Cases]. In Trudy 10-go mezhdunarodnogo nauchnogo seminara AMADE-2021 [Proc. 10th Intern. Workshop AMADE-2021] (104–116). Minsk: BSU, ITC of the Ministry of Finance. (In Russ., abstr. in Engl.). https://elib.bsu.by/handle/123456789/282282.

Mathai, A. M., & Saxena, R. K. (1978). The H-Function with Applications in Statistics and other Disciplines. New Delhi: Wiley Eastern; New York: Halsted Press. DOI: 10.2307/3314682.

Srivastava, H. M., Gupta, K. C., & Goyal, S. L. (1982). The H-Function of One and Two Variables with Applications. New Delhi: South Asian Publishers.

Prudnikov, A. P., Brychkov, Yu. A., & Marichev, O. I. (1990). Integrals and Series. More Special Functions. Vol. 3: More Special Functions. New York: Gordon and Breach.

Kilbas, A. A., & Saigo, M. H. (2004). H-Transforms. Theory and Applications. London [etc.]: Chapman and Hall. CRC Press.

Kiryakova V. (1994). Generalized Fractional Calculus and Applications. New York: Wiley and Son.

Katrakhov, V. V., & Sitnik, S. M. (1984). A boundary-value problem for the steady-state Schrodinger equation with a singular potential, Sov. Math. Dokl., 30(2), 468–470.

Sitnik, S. M. (1992). Factorization and estimates of the norm of Buschman-Erdeyi operators in weighted Lebesgue spaces. Sov. Math. Dokl., 44(2), 641–646.

Katrakhov, V. V., & Sitnik, S. M. (1995). Composition method for constructing B-elliptic, B-hyperbolic, and B-parabolic transformation operators. Russ. Acad. Sci., Dokl. Math., 50(1), 70–77.

Sitnik, S. M. (2017). A short survey of recent results on Buschman-Erdeyi transmutations. J. of Inequalities and Special Functions (Special issue to honor Prof. Ivan Dimovski’s contributions), 8(1), 140–157.

Skoromnik O. V. (2019). Integral'nye preobrazovanija s funkcijami Gaussa i Lezhandra v jadrah i integral'nye uravnenija pervogo roda. Novopolock: PSU. (In Russ.).

Katrakhov, V. V., & Sitnik, S. M. (2018). The transmutation method and boundary-value problems for singular elliptic equations. CMFD, 64(2). 211–426. DOI: 10.22363/2413-3639-2018-64-2-211-426.

Shishkina, E. L., & Sitnik S. M. (2020). Transmutations, singular and fractional differential equations with applications to mathematical physics. Elsevier.

Sitnik, S. M., & Shishkina, E. L. (2019). Transmutation Method for Differential Equations with Bessel Operators. Moscow: Fizmatlit.

Kravchenko V. V., Sitnik S. M. (Eds.). (2020). Transmutation Operators and Applications (Trends in Mathematics). Birkhauser.

Fitouhi, A., Jebabli, I., Shishkina, E. L., & Sitnik, S. M. (2018). Applications of integral transforms composition method to wave-type singular differential equations and index shift transmutations. Electron. J. Differential Equations, 2018(130), 1–27. DOI: 10.48550/arXiv.1805.06925.

Vu Kim Tuan, Marichev, O. I., & Yakubovich, S. B. (1986). On a boundary-value problem for elliptic equations of the second order at the sphere domain. Dokl. AN SSSR, 286(4), 786–790.

Marichev, O. I. (1978). Method evaluation of integrals of Special Functions (Theory and Formulas Tables). Minsk: Nauka i tekhnika.

Brychkov, Yu. A., Glaeske, H.-Y., Prudnikov, A. P., & Vu Kim Tuan. (1992). Multidimensional Integral Transformations. Philadelphia: Gordon and Breach.

Nikolski, S. M. (1975). Approximation of Functions of Many Variables and Embedding Theorems. Moscow: Nauka.

Rooney, P. G. (1983). On integral transformations with G-function kernels. Proc. Royal Soc. Edinburgh. Sect. A, (93), 265–297. DOI: 10.1017/S0308210500015973.

Rooney, P. G. (1994). On the range of the integral transformation. Canad. Math. Bul., 37(4), 545–548.

Rooney, P. G. (1995). On the representation of functions by the Hankel and some related transformations. Proc. Royal Soc. Edinburgh. Sect. A, 125(3), 449–463.

Sitnik S. M. (2009). Refinements and generalizations of classical inequalities. Studies in mathematical analysis. Series: Mathematical Forum, (3), 221–226.