TWO-DIMENTIONAL INTEGRAL TRANSFORM WITH THE MEIJER G-FUNCTION IN THE KERNEL IN THE SPACE OF SUMMABLE FUNCTIONS
Article Sidebar
Main Article Content
Abstract
Two-dimentional integral transform with the Meijer G-function in the kernel in the space of summable functions on a domain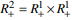 
was studied. 
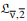-theory of a considered integral transformation was constructed. Conditions for the boundedness and one-to-one operator of such a transformation from one 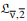-space to another were given, an analogue of the integration formula in parts was proved, various integral representations for the transformation under consideration were established. The results generalize the well know findings for corresponding one-dimentional integral transform.
Article Details
This work is licensed under a Creative Commons Attribution 4.0 International License.
References
Самко, С.Г. Интегралы и производные дробного порядка и некоторые их приложения / С.Г. Самко, А.А. Килбас, О.И. Маричев. – Минск : Наука и техника, 1987. – 688с.
Kilbas, A.A. H-Transforms. Theory and Applications / A.A. Kilbas, M.H. Saigo. – London [etc.] : Chapman and Hall. CRC Press, 2004. – 401 p.
Kilbas, A.A. Theory and applications of fractional differential equations. North – Holland Mathematics Studies 204 / A.A. Kilbas, H.M. Srivastava, J.J. Trujillo. – Amsterdam : Elsevier.xv, 2006. – 523 p.
Most read articles by the same author(s)
- O. SKOROMNIK, SOLUTION OF INTEGRAL EQUATIONS OF THE FIRST KIND WITH THE CONFLUENT HYPERDEOMETRIC FUNCTION AND NORMALIZED BESSEL FUNCTION IN THE KERNELS IN THE KLASS OF INTERGRABLE FUNCTIONS, Vestnik of Polotsk State University. Part C. Fundamental Sciences: No. 12 (2015)
- O. SKOROMNIK, Y. ZHAVORONOK, THE SOLUTION OF SOME INTEGRAL EQUATIONS WITH THE LEGENDRE FUNCTION IN KERNELS IN Lv,r - SPACES, Vestnik of Polotsk State University. Part C. Fundamental Sciences: No. 12 (2014)
- O. SKOROMNIK, Y. ZHAVORONOK, THE SOLUTION OF INTEGRAL EQUATIONS WITH THE GAUSS HYPERGEOMETRIC FUNCTION IN KERNELS IN Lv,r - SPACES, Vestnik of Polotsk State University. Part C. Fundamental Sciences: No. 4 (2014)