ОДНО ОБОБЩЕННОЕ H-ПРЕОБРАЗОВАНИЕ В ВЕСОВЫХ ПРОСТРАНСТВАХ ИНТЕГРИРУЕМЫХ ФУНКЦИЙ НА ПОЛУОСИ
##plugins.themes.bootstrap3.article.sidebar##
##plugins.themes.bootstrap3.article.main##
Аннотация
Изучены свойства одного класса обобщенных H-преобразований в весовых пространствах интегрируемых функций на полуоси. Получены условия ограниченности и взаимной однозначности операторов таких преобразования из одних пространств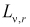 
в другие, доказаны аналоги формулы интегрирования по частям, получены различные интегральные представления для изучаемых преобразований, даны описания образов и выведены формулы их обращения.
##plugins.themes.bootstrap3.article.details##
Это произведение доступно по лицензии Creative Commons «Attribution» («Атрибуция») 4.0 Всемирная.
Библиографические ссылки
Kilbas, A. A. H-Transforms. Theory and Applications / A. A. Kilbas, M. H. Saigo. – London : Chapman and Hall. CRC Press, 2004. – 401 p.
Килбас, А. А. Обобщенное H-преобразование в весовых пространствах суммируемых функций / А. А. Килбас, Е. К. Щетникович // Весцi НАН Беларусi. Сер. фiз.-мат. навук. – 2004. – № 2. – С. 14–19.
Самко, С. Г. Интегралы и производные дробного порядка и некоторые их приложения / С. Г. Самко, А. А. Килбас, О. И. Маричев. – Минск : Наука и техника, 1987. – 688 с.
Рекомендуемые статьи автора (авторов)
- М. В. ПАПКОВИЧ, О. В. СКОРОМНИК, С. А. ШЛАПАКОВ, РЕШЕНИЕ ОДНОГО КЛАССА МНОГОМЕРНЫХ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ ПЕРВОГО РОДА С ФУНКЦИЕЙ ГИПЕРБОЛИЧЕСКОГО СИНУСА В ЯДРАХ, Вестник Полоцкого государственного университета. Серия С. Фундаментальные науки: № 12 (2021)
- С. М. СИТНИК, О. В. СКОРОМНИК, К. А. ВАСИЛЕВИЧ, ДВУМЕРНЫЕ ИНТЕГРАЛЬНЫЕ ПРЕОБРАЗОВАНИЯ С ФУНКЦИЕЙ КУММЕРА И ГИПЕРГЕОМЕТРИЧЕСКОЙ ФУНКЦИЕЙ ГАУССА В ЯДРАХ КАК ЧАСТНЫЕ СЛУЧАИ ДВУМЕРНОГО ИНТЕГРАЛЬНОГО G-ПРЕОБРАЗОВАНИЯ, Вестник Полоцкого государственного университета. Серия С. Фундаментальные науки: № 1 (2023)
- С. М. СИТНИК, О. В. СКОРОМНИК, М. В. ПАПКОВИЧ, ДВУМЕРНОЕ ИНТЕГРАЛЬНОЕ H-ПРЕОБРАЗОВАНИЕ В ВЕСОВЫХ ПРОСТРАНСТВАХ СУММИРУЕМЫХ ФУНКЦИЙ, Вестник Полоцкого государственного университета. Серия С. Фундаментальные науки: № 2 (2023)
- С. М. СИТНИК, О. В. СКОРОМНИК, М. В. ПАПКОВИЧ, ДВА ЧАСТНЫХ СЛУЧАЯ ДВУМЕРНОГО ИНТЕГРАЛЬНОГО G-ПРЕОБРАЗОВАНИЯ В ВЕСОВЫХ ПРОСТРАНСТВАХ СУММИРУЕМЫХ ФУНКЦИЙ, Вестник Полоцкого государственного университета. Серия С. Фундаментальные науки: № 11 (2022)
- М. В. ПАПКОВИЧ, О. В. СКОРОМНИК, ДВУМЕРНОЕ ИНТЕГРАЛЬНОЕ ПРЕОБРАЗОВАНИЕ С G-ФУНКЦИЕЙ МЕЙЕРА В ЯДРЕ В ПРОСТРАНСТВЕ СУММИРУЕМЫХ ФУНКЦИЙ, Вестник Полоцкого государственного университета. Серия С. Фундаментальные науки: № 4 (2019)
- О. В. СКОРОМНИК, ДВУМЕРНОЕ ИНТЕГРАЛЬНОЕ ПРЕОБРАЗОВАНИЕ С МОДИФИЦИРОВАННОЙ H-ФУНКЦИЕЙ В ПРОСТРАНСТВЕ СУММИРУЕМЫХ ФУНКЦИЙ, Вестник Полоцкого государственного университета. Серия С. Фундаментальные науки: № 4 (2018)
- О. В. СКОРОМНИК, Т. А. АЛЕКСАНДРОВИЧ, РЕШЕНИЕ МНОГОМЕРНОГО ИНТЕГРАЛЬНОГО УРАВНЕНИЯ ПЕРВОГО РОДА С ФУНКЦИЕЙ БЕССЕЛЯ – КЛИФФОРДА В ЯДРЕ ПО ПИРАМИДАЛЬНОЙ ОБЛАСТИ, Вестник Полоцкого государственного университета. Серия С. Фундаментальные науки: № 4 (2015)
- О. В. СКОРОМНИК, ДВУМЕРНОЕ ИНТЕГРАЛЬНОЕ ПРЕОБРАЗОВАНИЕ С ВЫРОЖДЕННОЙ ГИПЕРГЕОМЕТРИЧЕСКОЙ ФУНКЦИЕЙ КУММЕРА В ЯДРЕ И ИНТЕГРАЛЬНОЕ УРАВНЕНИЕ ПЕРВОГО РОДА В ПРОСТРАНСТВЕ СУММИРУЕМЫХ ФУНКЦИЙ, Вестник Полоцкого государственного университета. Серия С. Фундаментальные науки: № 4 (2017)
- О. В. СКОРОМНИК, ИНТЕГРАЛЬНЫЕ ПРЕОБРАЗОВАНИЯ С ВЫРОЖДЕННОЙ ГИПЕРГЕОМЕТРИЧЕСКОЙ ФУНКЦИЕЙ КУММЕРА И НОРМИРОВАННОЙ ФУНКЦИЕЙ БЕССЕЛЯ В ЯДРАХ И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО РОДА В ПРОСТРАНСТВЕ СУММИРУЕМЫХ ФУНКЦИЙ, Вестник Полоцкого государственного университета. Серия С. Фундаментальные науки: № 12 (2016)
- О. В. СКОРОМНИК, РЕШЕНИЕ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ ПЕРВОГО РОДА С ВЫРОЖДЕННОЙ ГИПЕРГЕОМЕТРИЧЕСКОЙ ФУНКЦИЕЙ И НОРМИРОВАННОЙ ФУНКЦИЕЙ БЕССЕЛЯ В ЯДРАХ В КЛАССЕ ИНТЕГРИРУЕМЫХ ФУНКЦИЙ, Вестник Полоцкого государственного университета. Серия С. Фундаментальные науки: № 12 (2015)