TWO SPECIAL CASES OF TWO-DIMENSIONAL INTEGRAL G-TRANSFORMATION IN THE WEIGHTED SPACES OF SUMMABLE FUNCTIONS
Article Sidebar
Main Article Content
Abstract
Two-dimensional integral transformations with special functions of the same type in kernels are considered. Using the Mellin transformation technique, it is shown that they are special cases of a two-dimensional G-transformation. Based on the theory of the G-transformation, the properties of the considered integral transformations in the weighted spaces of integrable functions in the domain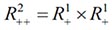 
are investigated. The results obtained generalize the data obtained for the corresponding one-dimensional analogues.
Article Details
This work is licensed under a Creative Commons Attribution 4.0 International License.
References
Papkovich, M. V., & Skoromnik, O. V. (2019). Dvumernoe integral'noe preobrazovanie s G-funktsiei Meiera v yadre v prostranstve summiruemykh funktsii [Two-Dimentional Integral Transform With the Meijer G-Function in the Kernel in the Space of Summable Functions]. Vestnik Polotskogo gosudarstvennogo universiteta. Seriya C, Fundamental'nye nauki [Herald of Polotsk State University. Series С. Fundamental sciences], 4(32), 131–136. (In Russ., abstr. in Engl.).
Papkovich, M. V., & Skoromnik O. V. (2020). Mnogomernoe integral'noe preobrazovanie s G-funktsiei Meiera v yadre v vesovykh prostranstvakh summiruemykh funktsii [Multidimensional integral transformation with Meijer's G-function in the kernel in the weighted spaces of summable functions]. In Z. Yu. Fazullin (Eds.) Ufimskaya osennyaya matematicheskaya shkola–2020: sb. tezisov [Ufa Autumn Mathematical School–2020] (142–144). – Ufa: Bashkir State University. (In Russ.)
Skoromnik, O. V., & Papkovich, M. V. (2022). Mnogomernye modifitsirovannye G-preobrazovaniya i integral'nye preobrazovaniya s gipergeometricheskoi funktsiei Gaussa v yadrakh v vesovykh prostranstvakh summiruemykh funktsii [Multidimensional modified G-transformations and integral transformations with hypergeometric Gauss functions in kernels in weight spaces of summed functions]. Vesnіk Vіtsebskaga dzyarzhaўnaga unіversіteta [Bulletin of VSU], 1(114), 11–25. (In Russ., abstr. in Engl.).
Sitnik S. M., Skoromnik, O. V., & Papkovich, M. V. (2022). Mnogomernye modifitsirovannye G- i H-preobrazovaniya i ikh chastnye sluchai [Multidimensional modified G- and H-transforms and their special cases]. In AMADE-2021: sb. trudov (104–116). Minsk: IVTs Minfina. (In Russ., abstr. in Engl.).
Sitnik, S. M., Skoromnik, O. V., & Shlapakov, S. A. (2019). Mnogomernoe obshchee integral'noe preobrazovanie so spetsial'nymi funktsiyami v yadre [Multidimensional general integral transformation with special functions in the kernel]. Vesnіk Vіtsebskaga dzyarzhaunaga unіversіteta [Bulletin of VSU], 3(104), 18–27. (In Russ., abstr. in Engl.).
Sitnik, S. M., & Skoromnik, O. V. (2020). One-dimensional and multi-dimensional integral transforms of Buschman- Erdelyi type with Legendre Functions in kernels. In Transmutation Operators and Applications. Trends in Mathematics (293–319). Cham, Switzerland: Birkhäuser Basel (Springer).
Samko, S. G., Kilbas, A. A., & Marichev, O. I. (1987). Integraly i proizvodnye drobnogo poryadka i nekotorye ikh prilozheniya [Integrals and derivatives of fractional order and some of their applications]. Minsk: Nauka i tekhnika.
Kilbas, A. A., & Saigo, M. H. (2004). H-Transforms. Theory and Applications. London [etc.]: Chapman and Hall. CRC Press.
Sitnik, S. M., Skoromnik, O. V., & Shlapakov, S. A. (2022). Multi-dimensional generalized integral transform in the weighted spaces of summable functions. Lobachevskii J. of Mathematics, 43(6), 1170–1178.
Kilbas, A. A., Srivastava, H. M., & Trujillo, J. J. (Ed.). (2006). Theory and applications of fractional differential equations. North–Holland Mathematics Studies (Vol. 204). Amsterdam: Elsevier.xv.
Most read articles by the same author(s)
- M. PAPKOVICH, O. SKOROMNIK, S. SHLAPAKOV, SOLUTION OF ONE CLASS OF MULTI-DIMENSIONAL INTEGRAL EQUATIONS OF THE FIRST KIND WITH HYPERBOLIC SINE FUNCTION IN KERNELS, Vestnik of Polotsk State University. Part C. Fundamental Sciences: No. 12 (2021)
- S. SITNIK, O. SKOROMNIK, Y. ARKHIPAVETS, ONE GENERALIZED H-TRANSFORMATION IN WEIGHT SPACES OF INTEGRATED FUNCTIONS ON A SEMI-AXIS, Vestnik of Polotsk State University. Part C. Fundamental Sciences: No. 12 (2021)
- S. SITNIK, O. SKOROMNIK, K. VASILEVICH, TWO-DIMENSIONAL INTEGRAL TRANSFORMATIONS WITH KUMMER FUNCTION AND HYPERGEOMETRIC GAUSSIAN FUNCTION IN KERNELS AS SPECIAL CASES OF TWO-DIMENSIONAL INTEGRAL G-TRANSFORMATION, Vestnik of Polotsk State University. Part C. Fundamental Sciences: No. 1 (2023)
- S. SITNIK, O. SKOROMNIK, M. PAPKOVICH, TWO-DIMENSIONAL INTEGRAL H-TRANSFORM IN WEIGHTED SPACES OF SUMMABLE FUNCTIONS, Vestnik of Polotsk State University. Part C. Fundamental Sciences: No. 2 (2023)
- PAPKOVICH PAPKOVICH, O. SKOROMNIK, TWO-DIMENTIONAL INTEGRAL TRANSFORM WITH THE MEIJER G-FUNCTION IN THE KERNEL IN THE SPACE OF SUMMABLE FUNCTIONS, Vestnik of Polotsk State University. Part C. Fundamental Sciences: No. 4 (2019)
- O. SKOROMNIK, TWO-DIMENTIONAL INTEGRAL TRANSFORM WITH THE H-FUNCTION IN THE KERNEL IN THE SPACE OF SUMMABLE FUNCTIONS, Vestnik of Polotsk State University. Part C. Fundamental Sciences: No. 4 (2018)
- O. SKOROMNIK, T. ALEKSANDROVICH, SOLUTION OF A MULTIDIMENSIONAL INTEGRAL EQUATION OF THE FIRST KIND WITH THE BESSEL – KLIFFORD FUNCTION IN THE KERNEL OVER A PYRAMIDAL DOMAIN, Vestnik of Polotsk State University. Part C. Fundamental Sciences: No. 4 (2015)
- O. SKOROMNIK, INTEGRAL TRANSFORMS WITH THE CONFLUENT HYPERDEOMETRIC FUNCTION OF KUMMER AND THE CUT BESSEL FUNCTION IN THE KERNELS AND INTEGRAL EQUATIONS OF THE FIRST KIND IN THE SPACE OF SUMMABLE FUNCTIONS, Vestnik of Polotsk State University. Part C. Fundamental Sciences: No. 12 (2016)
- O. SKOROMNIK, SOLUTION OF INTEGRAL EQUATIONS OF THE FIRST KIND WITH THE CONFLUENT HYPERDEOMETRIC FUNCTION AND NORMALIZED BESSEL FUNCTION IN THE KERNELS IN THE KLASS OF INTERGRABLE FUNCTIONS, Vestnik of Polotsk State University. Part C. Fundamental Sciences: No. 12 (2015)
- S. SITNIK, O. SKOROMNIK, A. KUROKHTINA, INTEGRAL TRANSFORMATION WITH THE MITTAG–LEFFLER FUNCTION IN SPACES OF LEBESGUE-MEASURABLE FUNCTIONS, Vestnik of Polotsk State University. Part C. Fundamental Sciences: No. 2 (2024)